
When there is a lot of data, it can be easier to separate the values into groups . We can then display the amount of data in each group in a grouped frequency table . We can also estimate the mean of a set of data from a grouped frequency table .
Make sure you are happy with the following topics before continuing:

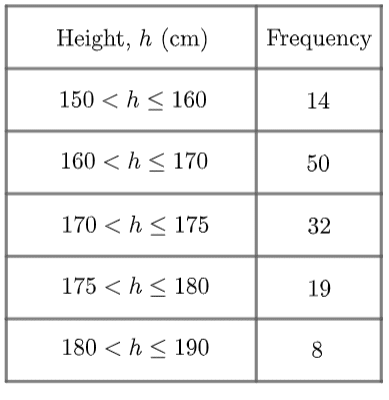
This particular example is a set of data on the heights of a selection of adults. To understand what this table is saying, let’s look at the first group (also known as a class):
This notation means that all people who fall within this group are
“taller than 150 cm but no taller than 160 cm.”
It’s important to understand that this group doesn’t include people who are exactly 150 cm tall, but it does include people who are exactly 160 cm tall.
This distinction matters, because we have to be clear about which group people on the edges of their class will fit into.
Level 6-7 GCSE Cambridge iGCSEThe signs used for the inequalities are important.
However, a \leq sign attached to a number means that the class does include that number. In the table above we can see that the class 150
The reason for this is so that the class boundaries fall into exactly one class .
If we used \leq only, some class boundaries would appear in two classes , so we wouldn’t know which class to put someone who is exactly 160\text < cm>tall in.
Since we don’t know exactly the values of data in a grouped frequency table , we cannot calculate an exact mean . Instead, we can use the information we do have to find an estimate for the mean . We can work out an estimate for the mean as follows.
Step 1: Add two new columns to the table, one called midpoint and one called midpoint \times frequency .
Step 2: In the midpoint column, add the midpoint of each class .
Step 3: To calculate the values for the midpoint \times frequency column, find the product of the frequency and midpoint for each row.
Step 4: Find the totals of the frequency column, and the midpoint \times frequency column.
Step 5: The estimate for the mean is the total of the midpoint \times frequency column, divided by the total of the frequency column.
Note: This is only an estimate . The real mean could vary substantially from this.
Example: Estimate the mean of the diameters of the pans sold in a kitchenware shop.

Step 1: Add two new columns to the table, one called midpoint and one called midpoint \times frequency .

Step 2: In the midpoint column, add the midpoint of each class .

Step 3: To calculate the values for the midpoint \times frequency column, find the product of the frequency and midpoint for each row.

Step 4: Find the totals of the frequency column, and the midpoint \times frequency column.
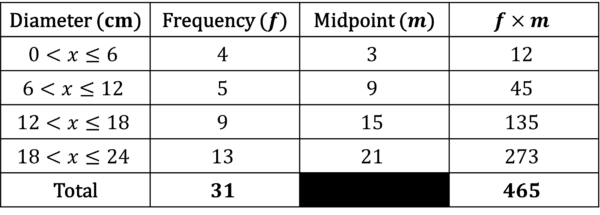
Step 5: The estimate for the mean is the total of the midpoint \times frequency column, divided by the total of the frequency column.
So the estimate for the mean is 15\text < cm>.